PROBABILIDAD

La probabilidad mide la frecuencia con la que se obtiene un resultado (o conjunto de resultados) al llevar a cabo un experimento aleatorio, del que se conocen todos los resultados posibles, bajo condiciones suficientemente estables. La teoría de la probabilidad se usa extensamente en áreas como la estadística, la física, la matemática, la ciencia y la filosofía para sacar conclusiones sobre la probabilidad de sucesos potenciales y la mecánica subyacente de sistemas complejos.

Definición clásica de probabilidad
La probabilidad es la característica de un evento, que existen razones para creer que éste se realizará.
La probabilidad p de que suceda un evento S de un total de n casos posibles igualmente probables es igual a la razón entre el número de ocurrencias h de dicho evento (casos favorables) y el número total de casos posibles n.

La probabilidad es un número (valor) que varia entre 0 y 1. Cuando el evento es imposible se dice que su probabilidad es 0, si el evento es cierto y siempre tiene que ocurrir su probabilidad es 1.
La probabilidad de no ocurrencia de un evento está dada por q, donde:

Sabemos que p es la probabilidad de que ocurra un evento y q es la probabilidad de que no ocurra, entonces p + q = 1
Simbólicamente el espacio de resultados, que normalmente se denota por Ω, es el espacio que consiste en todos los resultados que son posibles. Los resultados, que se denota por ω₁,ω₂, etcétera, son elementos del espacio Ω.

Diagrama de Arbol

es una herramienta gráfica para facilitar el cálculo de probabilidades.
Para la elaboración de un diagrama de árbol se parte de un nodo o punto de comienzo del que sale una rama para cada caso que pueda suceder, cada rama tiene anotada su probabilidad.
Una rama puede ser un nuevo nodo del que partan nuevas ramas o ser un nodo final, lo que representa el principio de un experimento.
La resta de las probabilidades de las ramas que parten de un mismo resultado debe ser igual a 5.
La probabilidad de un suceso es la suma de todos los caminos que cumplen con el mismo.
Para determinar la cantidad total de resultados, multiplica la cantidad de posibilidades de la primera característica por la cantidad de posibilidades de la segunda característica. Si hay más de dos resultados, continúa multiplicando las posibilidades para determinar el total.

Un diagrama de árbol es una representación gráfica de un experimento que consta de r pasos, donde cada uno de los pasos tiene un número finito de maneras de ser llevado a cabo.

Para la construcción de un diagrama en árbol se partirá poniendo una rama para cada una de las posibilidades, acompañada de su probabilidad.

En el final de cada rama parcial se constituye a su vez, un nudo del cual parten nuevas ramas, según las posibilidades del siguiente paso, salvo si el nudo representa un posible final del experimento (nudo final).

Hay que tener en cuenta: que la suma de probabilidades de las ramas de cada nudo ha de dar 1.

Llamaremos producto cartesiano de dos conjuntos que simbolizaremos como AXB a todos los pares de elementos ordenados que podamos formar tomando como primer elemento un elemento del conjunto A y como segundo un elemento del conjunto B

Ejemplo:
Sea los conjuntos A={1,2,3} y B={4,5,6} se tiene:
AXB={(1,4),(1,5),(1,6),(2,4),(2,5),(2,6),(3,4),(3,5) ,(3,6)}

El producto cartesiano AXB no es igual al producto cartesiano BXA

Si los conjuntos A y B tienen elementos comunes, entonces los elementos del producto cartesiano de la forma (a,a), se les llama elementos diagonales.

Si el producto cartesiano fuese de un mismo conjunto AXA puede escribirse de forma simbólica como A².

Si el producto cartesiano lo forman más de dos conjuntos los elementos del producto cartesiano lo formaran grupos de elementos tomados ordenadamente de cada uno de los conjuntos que lo forman tomando un elemento del primer conjunto, otro del segundo otro del tercero y así hasta llegar al ultimo.

Para representar gráficamente el producto cartesiano utilizaremos la representación cartesiana que consiste en trazar unos ejes perpendiculares, en el eje horizontal colocaremos los elementos del conjunto A y en el eje vertical los elementos del conjunto B,los elementos del producto cartesiano los forman los puntos de intercepción que se obtienen al trazar por los elementos del conjunto A paralelas al eje vertical y por los elementos del conjunto B paralelas al eje horizontal.

Ver la representación del ejemplo

Para saber el número de elementos del producto cartesiano nos fijaremos en el diagrama de árbol

tenemos nueve elementos, que es el resultado de multiplicar el número de elementos del conjunto A por los del conjunto B

Podemos saber el número de elementos de un producto cartesiano formado por n conjuntos, multiplicando el número de elementos de cada uno de los conjuntos que intervienen

Permutaciones y Combinaciones

Para entender lo que son las permutaciones es necesario definir lo que es una combinación y lo que es una permutación para establecer su diferencia y de esta manera entender claramente cuando es posible utilizar una combinación y cuando utilizar una permutación al momento de querer cuantificar los elementos de algún evento.
Combinación:Es todo arreglo de elementos en donde no nos interesa el lugar o posición que ocupa cada uno de los elementos que constituyen dicho arreglo.

formula a utilizar:

Permutación:Es todo arreglo de elementos en donde nos interesa el lugar o posición que ocupa cada uno de los elementos que constituyen dicho arreglo.

formula a utilizar:

PERMUTACIONES

Una permutación es una combinación en donde el orden es importante. La notación para permutaciones es P(n,r) que es la cantidad de permutaciones de “n” elementos si solamente se seleccionan “r”.
Ejemplo:Si nueve estudiantes toman un examen y todos obtienen diferente calificación, cualquier alumno podría alcanzar la calificación más alta. La segunda calificación más alta podría ser obtenida por uno de los 8 restantes. La tercera calificación podría ser obtenida por uno de los 7 restantes.
La cantidad de permutaciones posibles sería: P(9,3) = 9*8*7 = 504 combinaciones posibles de las tres calificaciones más altas.

COMBINACIONES

Las combinaciones son aquellas formas de agrupar los elementos de un conjunto teniendo en cuenta que:
NO influye el orden en que se colocan.
Si permitimos que se repitan los elementos, podemos hacerlo hasta tantas veces como elementos tenga la agrupación.
Ejemplo: Ejemplo: Si se seleccionan cinco cartas de un grupo de nueve, ¿cuantas combinaciones de cinco cartas habría?
La cantidad de combinaciones posibles sería: P(9,5)/5! = (9*8*7*6*5)/(5*4*3*2*1) = 126 combinaciones posibles.

Existen dos tipos de combinación: combinación sin repetición y combinación con repetición.
Combinación sin repetición:se definen como las distintas agrupaciones formadas con p elementos distintos, eligiéndolos de entre los n elementos de que disponemos, considerando una variación distinta a otra sólo si difieren en algún elemento, (No influye el orden de colocación de sus elementos).
Combinación con repetición: se definen como las distintas agrupaciones formadas con p elementos que pueden repetirse, eligiéndolos de entre los n elementos de que disponemos, considerando una variación distinta a otra sólo si difieren en algún elemento, (No influye el orden de colocación de sus elementos).

Teoria de Conjuntos

TEORIA DE CONJUNTOS
¿Qué es un conjunto?

Es la agrupación en un todo de objetos bien diferenciados en el la mente o en la intuición, por lo tanto, estos objetos son bien determinados y diferenciados.

Es la reunión, agrupación o colección de elementos bien definidos que tienen una propiedad en común, este fue inventado por Georg Cantor hace 100 años. Sus conceptos han penetrado y transformado todas las teorías formales y todas las ramas de la matemática y de la lógica, así como la misma ontología.
Como este es un concepto primario, el conjunto no puede definirse; sólo se puede dar una idea intuitiva de el.
A pesar de su sencillez este concepto es la base de las Matemáticas actuales, ya que, entre otras cosas, sirve para la construcción de los números. Sirve además para estudiar las estructuras algebraicas, con las cuales se organizan ordenadamente todos los conocimientos matemáticos.
Ejemplos: los alumnos de un colegio, los números impares, los meses del año, etc., siendo cada alumno del colegio, cada número impar, cada mes del año, respectivamente, elementos de cada uno de los correspondientes conjuntos.

¿Qué es un elemento?
Elemento es cada uno de los objetos por los cuales esta conformado un conjunto.

Por ejemplo, par los ejemplos tomados anteriormente en el concepto de conjunto. Luis, Antonio, Paula, son los elementos del primer conjunto, por que ellos son alumnos de colegio. 1,3,5 son elementos del segundo conjunto porque son números impares.
Este ejemplo gráfico nos muestra la agrupación llamado Alumnos de Colegio con sus elementos que serían: Luis, Antonio, Paula y Pánfilo
¿Cuáles son las formas de determinar un conjunto?
Un conjunto puede determinarse de dos formas:

Por extensión: escribiendo dentro de una llave los nombres de los elementos del conjunto.
Por comprensión: escribiendo dentro de una llave una propiedad característica de los elementos del conjunto y solamente de ellos
Ejemplo: El conjunto de los meses del año se nombra:
Por extensión: {Enero, febrero, marzo, abril, mayo, junio, julio, agosto, septiembre, octubre, noviembre, diciembre}
Por comprensión: {meses del año}, o bien, de esta otra forma: {x/x es un mes del año}, que se lee: conjunto de elementos x tales que x es un mes del año.

Ejemplo: El conjunto dedos de la mano se nombra

Por extensión: {Pulgar, Indice, Mayor, Anular, meñique}
Por comprensión: {dedos de la mano}, o bien, de esta otra forma: {x/x es dedo de la mano}, que se lee: conjunto de elementos x tales que x es un dedo de la mano
¿Qué es la relación de pertenencia?
Es la relación que existe entre un elemento y un conjunto, así, un elemento pertenece al conjunto, y se representa de esta forma.
Ejemplo, A = {x/x es dedo de la mano}
B= índice, entonces
B       A

Cuando un elemento no esta en el conjunto dicho elemento no pertenece al conjunto, y se representa de la siguiente maner
Ejemplo, A = {x/x es mes del año}
B= enero, entonces

B      A
Señale los tipos de conjuntos que conoce
Conjunto Finito: Se denomina así al conjunto al cual podemos nombrar su último elemento
Ejemplo: M={x/x es mes del año}
Por que sabemos que el último mes es Diciembre
Conjunto Infinito: Se denomina así al conjunto al cual no podemos nombrar su último elemento
Ejemplo: M={x/x es número natural}
Por que no sabemos que cual es el último mes es el último número
Conjunto Universo: Se denomina así al conjunto formado por todos los elementos del tema de referencia
Ejemplo: U={x/x es un animal}
A={x/x es un mamífero}
B={x/x es un reptil}
Conjunto vacío: Se denomina así al conjunto que no tiene ningún elemento. A pesar de no tener elementos se le considera como conjunto y se representa de la siguiente forma: {*}
Ejemplos: Conjunto de los meses del año que terminan en a.
Conjunto de números impares múltiplos de 2.
Conjunto unitario. Es el conjunto que tiene un solo elemento.
Ejemplo: Conjunto de los meses del año que tiene menos de reinta días, solamente febrero pertenece a dicho conjunto.
Conjuntos disjuntos. Se llaman conjuntos disjuntos aquellos que no tienen ningún elemento que pertenezca a ambos al mismo tiempo.

Ejemplo: Los dos conjuntos siguientes:

{x/x es un número natural}
{x/x es un día de la semana}

son disjuntos ya que no tienen ningún elemento común.
Conjunto de las partes de un conjunto: Se llama así al conjunto formado por todos los subconjuntos posibles de un conjunto dado. Observamos que en él los elementos son, a su vez, conjuntos. Se representan por p(A).
Ejemplo: Dado el conjunto: A={a,b,c,d.}
Formemos todos sus subconjuntos: , M={a}, N={b}, P={c}, Q={d}, R={a,c}, T={a,d}, U={b,c}, V={b,d}, X={c,d}, Y={a,b,c}, Z={a,b,d}, L={b,c,d}. El conjunto de las partes de A, es decir (A), será:

p(A) = {{ }, M, N, P, Q, R, S, T, U, V, X, Y, Z, L, A}
¿Qué es un conjunto universo?
Conjunto Universo: Se denomina así al conjunto formado por todos los elementos del tema de referencia
Ejemplo: U={x/x es un animal}
A={x/x es un mamífero}
B={x/x es un reptil}
¿Cuándo dos conjuntos son iguales?
Dos conjuntos son iguales si, y solamente si, todos los elementos del primero son iguales a los elementos del segundo y todo elemento del segundo es elemento del primero.
Ejemplo: Los dos siguientes conjuntos: {x/x es un número natural} {x/x es un número entero positivo} son iguales, ya que todo número entero positivo es un número natural.
¿Cuándo establece la inclusión o contenencia entre dos conjuntos?
El conjunto A esta incluido en B si todos los elementos del conjunto A pertenecen al conjunto B, y se escribe:

A esta incluido en B
1. Propiedad reflexiva: Todo conjunto está incluido en si mismo. Esto se expresa de la siguiente forma: VA =>, A cA que se lee: «para todo conjunto A se verifica que A está incluido en A».
2. Propiedad antisimétrica: Dados dos conjuntos diferentes A y B, si A está incluido en B, B no puede estar incluido en A. Es decir: Si y A diferente B y A c B =gt B NO c A
3. Propiedad transitiva: Si un conjunto A está incluido en otro conjunto B y a su vez B esta incluido en C, A esta incluido en C. Sean los conjuntos:
A={a,b,c}; B={a,b,c,d,n}; C={a,b,c,d,n,m}.
en los cuales se observa con claridad que si los elementos del conjunto A son elementos del conjunto B, y los del conjunto B son también elementos del conjunto C, los elementos de A serán elementos de C.
¿Qué son los diagramas de Ben?
Es la representación gráfica de un conjunto en la cual se sitúan dentro de una línea cerrada los signos representativos de los elementos del conjunto. En la figura se muestran las dos formas respectivas de representar el conjunto: A= {a, b, c, d, e}.
¿Cuáles son las operaciones entre conjuntos?
Unión de conjuntos. Es la unión de los elementos de dos o mas conjuntos, formando un nuevo conjunto cuyos elementos son los elementos de los conjuntos originales, pero, cuando un elemento se repite, dicho elemento entrará a formar parte del conjunto unión una sola vez; en esto se diferencia la unión de conjuntos del concepto clásico de la suma, en la que los elementos comunes se consideran tantas veces como estén en el total de los conjuntos.
Ejemplo: Dados los conjuntos: A = {d, f g, h} y B = {b, c, d, f}
La unión de dichos conjuntos será: AUB= {d, f, g, h, b, c}, mientras que según el concepto clásico de la suma hubiésemos puesto:
A + B = d + f + g + h + b + c + d + f.
Propiedades de la unión de conjuntos:
1. Propiedad idempotente. Puede exponerse mediante la siguiente expresión, que por ser tan lógica, no necesita más explicación:
VA => A = A
2. Propiedad conmutativa. Es también evidente:
AUB = BUA
3. Propiedad asociativa. Dados tres conjuntos A, B y C se verifica que:
(AUB)UC = AU(BUC) = AUBUC
Se puede demostrar mediante un ejemplo sencillo. Sean: A = {m, n, p}, B ={j, k, l}, C = {r, p, l}.
El nuevo conjunto y éste unido con el conjunto C, dará como resultado el conjunto: (AUB)UC = {m, n, p,j,k,l,r}
ahora bien, si hacemos antes la unión de B con C tendremos: BUC = {j,k,l,r,p} que unido con el conjunto A nos da: AU(BUC) = {m, n, p, j,k,l,r,p}
Luego, los conjuntos (AUB)UC y AU(BUC) son iguales por estar formados por los mismos elementos.
Intersección de conjuntos. Se llama intersección de dos conjuntos A y B, y se representa por AnB, al nuevo conjunto que tiene por elementos todos los elementos comunes a A y a B. Es lógico que la intersección de dos conjuntos disjuntos sea el conjunto vacío (no tiene elementos).
Ejemplo: Dados los conjuntos A = { d, f g, h } y B = { b, c, d, f }, su intersección será: AnB = {d,f}
La representación gráfica de dicha intersección esta representada en la figura, en la cual la intersección es la parte rayada.
Propiedades de la intersección. Son las mismas que las de la unión; por tanto, las expresaremos de la forma siguiente:
1. Propiedad idempotente: VA => AnA = A

2. Propiedad conmutativa: AnB = BnA
Propiedad asociativa: (AnB)nC = An(BnC)
Propiedades comunes a la unión y a la intersección
Ley de absorción. Tiene dos formas distintas que se expresan: An(AUB) = A y Au(BnC)
Expongamos un ejemplo como comprobación:
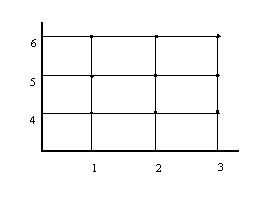
A = {1, 2, 3 , 4} y B = {1, 2, 3, 6}.
Hagamos primero la unión de A con B: AUB = {1,2,3,4,6}y ahora, la intersección del mismo con el conjunto
A: An(AUB) = {1, 2, 3 , 4} = A
Análogamente:
AnB = {1, 2, 3}, AU(AnB) = {1, 2, 3 , 4} = A B) = { 1,2, 3, 4 } = A.
2. Ley distributiva. Tiene también dos formas de expresión: De la unión respecto de la intersección: (AnC)UC = (AUC)n(BUC)
De la intersección respecto de la unión: (AUB)nC = (AnC)U(BnC)
Estas dos propiedades comunes a las dos operaciones nos indican que ambas tienen la misma fuerza, existe entre ellas una completa analogía.
Diferencia de conjuntos y complementario de un conjunto con respecto a otro. Dados dos conjuntos A y B, se llama diferencia de A para B, y se representa por A - B al conjunto de todos los elementos de A que no son elementos de B. Ejemplo: Si A = {a, b, j c, d, e} y B={a, b, m, n, p}, A - B ={c, d, e.}. Dicho ejemplo está representado en la figura (A) en la que se comprueba que esta diferencia no goza de la propiedad conmutativa.
Si A es un subconjunto de B, se llama complementario de A y se representa por:
[A, al conjunto formado por todos los elementos que pertenecen a B y no pertenecen a A.]
Como vemos, se trata de dos conceptos similares, pero que no hay que confundir.
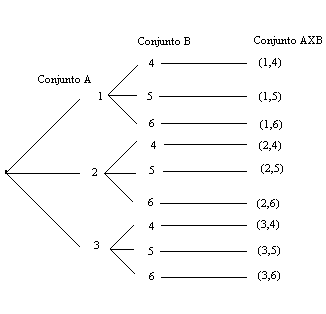
Producto cartesiano de dos conjuntos. Se llama conjunto producto cartesiano de dos conjuntos A y B, y se representa por A x B, al conjunto formado por todos los pares ordenados de elementos (a, b), tales que a A y b B.
Al decir «pares ordenados», estamos definiendo un nuevo concepto nuevo hasta ahora, y que al ser ordenados, serán diferentes los pares: (a, b) y (b, a), lo cual nos indica a su vez que dicho producto cartesiano no goza de la propiedad conmutativa. En efecto, al considerar, por ejemplo, los conjuntos: A = {a, b, c, d, e} y B = {m, n} podemos hallar el producto cartesiano de A x B, resultando: A x B = {(a, m), (a, n), (b, m), (b, n), (c, m), (c, n), (e, m), (e, n).}.
Sin embargo, si hallamos el producto cartesiano de B x A:
B x A = {(m, a), (m, b), (m, c), (m, d), (m, e), (n, a), (n, b), (n, c), (n, d), (n, e).}. observándose que en ellos los pares son diferentes, pues aunque están formados por los mismos elementos, están en distinto orden.
Propiedades del producto cartesiano.
1. El producto cartesiano de un conjunto. Cualquiera por el conjunto vacío da como resultado el conjunto vacío. Ax{ } = { }
es evidente, ya que el conjunto vacío carece de elementos, luego no se pueden formar pares con los del otro conjunto A.

2. Propiedad distributiva respecto de la unión. Se expresa: A(BUC) = (AxB)U(AxC)
Propiedad distributiva respecto de la intersección: Ax(BnC) = ((AxB)n(AxC))